[PyTorch] 선형 회귀 모델 학습 | 난수 고정, CUDA, NCHW, 손실 함수, 경사하강법
오늘부터 파이토치로 딥러닝 공부 시작 - !
본격적인거니까 잘 따라가봐야겠다.
import torch
# nn : Neural Network
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim이렇게 임포트를 해왔음
# pytorch에 난수 발생기 -> 1로 고정
# 실행시 pytorch의 난수를 고정 -> 동일한 결과를 얻기
torch.manual_seed(1)이 코드에서 궁금한 점이 많이 생겨서 찾아봤다.
왜 난수를 고정하는가?
→ 결과의 재현성(reproducibility)때문
딥러닝/머신러닝에서 모델 가중치 초기화, 데이터 셔플링, 미니 배치구성 등과 같은 모델의 학습이나 평가 중에 난수가 많이 사용된다.
같은 코드라도 실행할 때마다 다른 결과를 생성할 수도 있는데, 난수를 고정하면 실험을 반복하거나 다른 사람과 코드를 공유할 때 일관된 결과를 보장할 수 있고 디버깅이 용이하다.
GPU환경에서는 왜 코드가 다른가?
CUDA(Compute Unified Device Architecture)는 NVIDIA가 개발한 GPU 프로그래밍 플랫폼이다.
GPU는병렬 처리가 강력하므로, 딥러닝 모델을 학습하거나 추론할 때 CPU에 비해 훨씬 빠르게 계산을 수행할 수 있다.
- PyTorch와 CUDA
# GPU에서는 이렇게 사용한다.
torch.cuda.manual_seed(1)
# CPU, GPU 환경에서 일관된 결과를 얻기 위해서는 ...
import torch
# CPU와 CUDA 모두에서 동일한 난수를 발생시키기 위한 설정
torch.manual_seed(1)
if torch.cuda.is_available():
torch.cuda.manual_seed(1)
# 결정론적(deterministic)방법 사용(같은 입력에 대해항상동일한 결과 반환 강제)
torch.backends.cudnn.deterministic = True
# 알고리즘 중 가장 빠른 것 선택, 항상 동일한 알고리즘 사용(일관성ㅇㅇ)
torch.backends.cudnn.benchmark = False
# 예시 텐서 생성
random_tensor = torch.rand(2, 2)
print(random_tensor)딥러닝 모델의 가중치를 GPU에서 초기화하거나, 데이터 전처리 과정에서 GPU 상에서 무작위적인 연산이 이루어질 수 있다.
이런 경우 GPU에서의 재현성을 보장하려면 CUDA 난수 발생기도 고정해야 한다.
기본적으로 PyTorch는 NCHW 형태라고 하는데, NCHW 형태란?
PyTorch에서 기본적으로 사용하는 NCHW 형태는 배치(batch)데이터의 텐서(tensor) 형식을 나타내는 방식이다.
이 용어는 딥러닝에서 주로 사용하는 이미지 데이터의 형식을 나타내며, 각각의 글자가 데이터의 차원을 뜻한다.
N: Batch Size (데이터의 개수)
- 하나의 미니배치에 포함된 이미지 또는 데이터의 개수를 의미한다. (32면 한 번에 32개 이미지 처리)
C: Channel (채널)
- 이미지의 채널 수를 나타낸다.
- 흑백: 1개(그레이스케일)
- 컬러(RGB): 3개
H: Height (이미지의 세로 길이)
- 이미지의 세로 방향 픽셀 수를 의미한다.
W: Width (이미지의 가로 길이)
- 이미지의 가로 방향 픽셀 수를 의미한다.
예시)
만약 32개의 3채널(RGB) 이미지가 있고, 이미지의 크기가 64 x 64라면, PyTorch에서 사용하는 텐서의 형태는 (32, 3, 64, 64)가 된다.
왜 NCHW 형태를 사용하는가?
1. GPU의 효율성
GPU에서 병렬 처리를 최적화하는 데 적합한 메모리 배열 방식이다.
2. 채널 우선
채널(C)이 먼저 나오므로, 특정 연산을 할 때 채널별 처리가 더 효율적이다.
추가) Tensorflow에서는 NHWC 형식(Batch, height, width, channel)을 사용한다.
Weight Initialization
# torch type으로 1개 파라미터를 0으로 초기화
# 학습시에 업데이트를 하는 가중치(해당 텐서가 학습 가능한 파라미터임을 나타냄)
W = torch.zeros(1, requires_grad=True)
print(W) # [0.]
b = torch.zeros(1, requires_grad=True)
print(b) # [0.]딥러닝 모델의 가중치(Weight)와 바이어스(Bias)를 초기화하는 방식이다.
requires_grad=True 는 학습 시에 경사(gradient)를 계산하여 업데이트되는 가중치 파라미터임을나타낸다.
텐서가 역전파(backpropagation)과정에서 경사도(gradient)를 계산하고, 이를 통해 값이 업데이트될 수있도록 만든다.
왜 requires_grad=True가 중요한지?
→ PyTorch에서 자동 미분(Autograd) 시스템을 활성화하는데 중요한 역할을 한다.
이 옵션이 설정된 텐서는 역전파를 통해 손실 함수(loss)의 경사도를 계산할 수 있으며, 경사도에 따라 파라미터가 업데이트된다.
- Forward Propagation: 데이터를 입력으로 받아 계산된 출력 값을 얻는다.
- Backward Propagation: 출력 값과 실제 값 간의 손실을 계산한 후, 역전파를 통해 각 파라미터(W, b 등)의 경사도를 계산하고, 이를 이용해 파라미터를 업데이트한다.
w와 b
- W = torch.zeros(1, requires_grad=True) : w는 0으로 초기화된 가중치(weight)파라미터이다. 딥러닝 모델에서 가중치는 학습 중에 최적화되며, 역전파를 통해 그 값이 조정된다.
- b = torch.zeros(1, requires_grad=True) : b는 0으로 초기화된 바이어스(bias) 파라미터이다. 바이어스는 가중치에 더해져 모델의 출력에 영향을 미친다. 이 역시 학습 중에 조정되는 파라미터이다.
Hypothesis

hypothesis = x_train * W + b
print(hypothesis)선형 회귀 모델의 가설(hypothesis)을 나타낸다.
이는 주어진 입력 데이터 x_train에 대해 예측하는 값을 계산하는 수식이다.
Cost
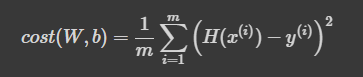
cost = torch.mean((hypothesis - y_train) ** 2)
print(cost)선형 회귀 모델에서 손실 함수(Loss function)를 계산하는 부분으로, 모델이 예측한 값(hypothesis)과 실제 값(y_train) 간의 차이를 기반으로 평균 제곱 오차(MSE, Mean Squared Error)를 구한다.
손실 값이 작을수록 모델의 예측이 더 정확하다는 것을 의미하며, 학습 과정에서 이 손실 값을 줄이는 것이 목표다.
Gradient Descent
# 경사하강법을 통해 모델의 w와 b를 계산하여 업데이트하는 과정이다.
optimizer = optim.SGD([W, b], lr=0.01)
# 기울기를 계산하기 전에 기울기를 0으로 초기화
optimizer.zero_grad()
# 오차 역전파법으로 w, b값을 업데이트 (손실함수(cost)에 대한 기울기 자동 계산)
cost.backward()
# 한걸음 이동(이동하는 크기는 기울기와 학습률에 의해 결정된다)
optimizer.step()
print(W)
print(b)여기서 기울기를 0으로 초기화하는 이유는?
PyTorch에서는 역전파를 할 때 기울기가 누적되기 때문에, 매번 새로운 기울기를 계산하기 전에 기울기를 초기화해야 한다.
SGD란?
확률적 경사하강법(Stochastic Gradient Descent)으로 최적화 알고리즘이다.
전체 데이터셋이 아닌 무작위로 선택된 일부분(미니배치)을 사용하여 경사하강법을 수행한다.
lr=0.01 : 학습률(learning rate)로, 경사하강법에서 파라미터를 업데이트할 때, 얼마나 큰 폭으로 이동할지를 결정한다.
경사하강법의 학습 과정 요약
- 손실 함수 계산: 먼저, 현재의 가중치와 바이어스로 모델의 예측값(hypothesis)을 계산하고, 이 예측값과 실제 값(y_train) 간의 차이를 이용해 손실 함수(cost)를 계산한다.
- 기울기 계산: 역전파를 통해 손실 함수의 가중치와 바이어스에 대한 기울기(gradient)를 계산한다.
- 기울기 초기화: 기울기 계산 전, 누적된 기울기를 optimizer.zero_grad()로 0으로 초기화한다.
- 파라미터 업데이트: 계산된 기울기를 사용하여 경사하강법 한 스텝을 진행하고, W와 b를 업데이트합니다.
- 반복: 이 과정을 반복하면서 손실 함수가 점점 줄어들고, 최적의 W와 b에 가까워집니다.
선형 회귀 모델 학습 예제 전체 코드
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01)
# 훈련 반복(Epochs): 1000번의 반복 학습 설정
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Forward Propagation (H(x) 계산)
hypothesis = x_train * W + b
# cost 계산 (손실 함수) -> 평균 제곱 오차(MSE) 구하기
cost = torch.mean((hypothesis - y_train) ** 2)
# Backpropagation과 Optimization (cost로 H(x) 개선)
# 역전파 -> 손실 함수의 기울기를 계산
# 최적화 -> W와 b를 경사 하강법으로 한 스텝 업데이트
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번의 에포마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))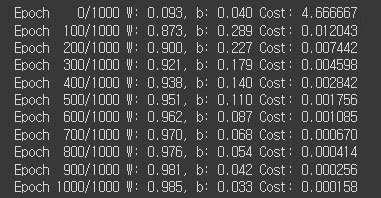
주어진 데이터에 대해 경사하강법을 적용하여 가중치(W)와 바이어스(b)를 최적화하는 과정을 보여준다.
PyTorch를 사용한 선형 회귀 모델 학습 예제
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
# 선형 회귀 모델을 정의하는 클래스
# 내부적으로 가중치(W)와 바이어스(b)가 포함된 선형 회귀 방정식을 사용해 예측값을 계산
model = LinearRegressionModel()
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.01)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
# 평균 제곱 오차(MSE) 계산
cost = F.mse_loss(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
params = list(model.parameters())
W = params[0].item()
b = params[1].item()
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W, b, cost.item()
))